Április egyszerre a költészet és a matematika hava – hogyan is lehetne szebben ünnepelni, mint egy számsorozaton alapuló versformával? Egy kaliforniai forgatókönyvíró fibnek nevezi találmányát, azt a versfajtát, amelyeknek soronkénti szótagszáma 1–1–2–3–5–8. Gregory K. Pincus a blogján gyűjti a kísérleteket.
„Ez
vers.
Ilyet
mindenki
gyárthat magának
Fibonacci-sorozatból.”
A fenti zsenge poétikai szempontból teljességgel értéktelen, egy érdekessége mégis van: Gregory K. Pincus kaliforniai forgatókönyvíró találmányán, a Fibonacci-strófán alapul. Pincusnak egy 2005-ös írótalálkozón jutott eszébe, hogy kellene egy olyan versforma, amely „precízebb” az 5–7–5 szótagból álló, japán eredetű haikunál – bármit is jelentsen a költészetben a fokozott precizitás.
A matek iránt érdeklődő forgatókönyvíró hamarosan rátalált a híres Fibonacci-sorozatra, és megalkotta a vonatkozó versstrófát, amelyet a híres sorozatnak megfelelő szótagszámú sorokra épül, és elméletileg a végtelenségig folytatható.
Nyolc sorban mondom el
A feltaláló a Fibonacci-sorozatra épülő verseket Fibeknek nevezte el, és blogján gyűjti a költőjelöltek kísérleteit, amelyek között vannak ígéretesek és szemétre valók is. Egyetlen közös jellemzőjük a forma: minden sor szótagszámát az előző két sor szótagainak összege adja. Egy Fib első sora elméletileg a 0 (ez természetesen nem jelenik meg a versben), a második 1, a harmadik sor szintén 1 szótagos (0+1), a negyedik 2 (1+1), és így tovább, egészen a végtelenségig, bár a költők legtöbbje megáll a hatodik, nyolc szótagos sornál, mint ez a tehetséges versenyző is:
“Sex.
Docs.
Troubles.
Medicine.
Grey’s Anatomy:
You are my Sunday night pleasure.”
Nyolcszáz éves sorozat
A szóban forgó számsorozatot először 1150-ben írta le két indiai matematikus, de nevét a Fibonacciként ismert Pisai Leonardóról, a XII. század végén született itáliai matematikusról kapta. Fibonacci az indiai tudósoktól függetlenül, egy nyulak szaporodásával kapcsolatos elméleti jellegű probléma kapcsán írta le a számokat Liber Abaci című munkájában 1202-ben.
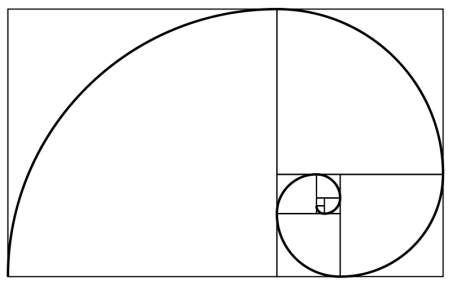
\begin{aligned} f(1) & = f(2) = 1 \\ f(n) & = f(n-1) + f(n-2) \enspace \enspace (n \ge 3) \\ \end{aligned}A Fibonacci-számok (0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, … stb.) lineárisan rekurzív sorozatot alkotnak, és azért különösen érdekesek, mert a természetben is megfigyelték őket: ilyen szekvenciákba szerveződnek egyes fűszálak, virágok, fa- és bokorágak, de a Fibonacci-sorozatoknak megfeleltethetően nő a fenyőtoboz, az ananász, a málna és a brokkoli is.
A nevezetes számok sok irodalmárt is megihlettek, sőt egyes feltételezések szerint magát Bartók Bélát sem hagyták nyugton. A szerző egyik értő kutatója, Lendvai Ernő szerint Bartók Zene húros hangszerekre, ütőkre és cselesztára című művének 88 ütemes Andante tranquillo tétele a Fibonacci-sorozat hatását mutatja (az indoklás szerint a 88 majdnem 89, amely Fibonacci-szám). Vannak olyan vélekedések is, amelyek szerint „Bartók zenéjében minden ezekre az egész számokra épül”.



