Arthur király udvarában 150 nőtlen lovag és 150 hajadon vendégeskedett. A király elhatározta, hogy összeházasítja őket. A világraszóló lakodalom azonban komoly akadályba ütközött: a hölgyek és urak némelyike ki nem állhatta egymást, így közöttük nemhogy házasság, de még egy beszélgetés sem jöhetett szóba. Arthur többször is próbálkozott, de minden alkalommal kudarcot vallott. Előhívta hát Merlint, a varázslót, és megparancsolta neki: házasítsa össze a vendégeket úgy, hogy a frigy egyetlen párnak se legyen ellenére. A természetfölötti képességekkel rendelkező mágus egy pillantás alatt átlátta, hogy a 150!1 lehetséges párosítás mindegyikében akadnak össze nem férő felek, és ezt azon nyomban közölte is a királlyal. Mivel azonban Merlin nem csupán nagy varázsló, de meglehetősen kétes alak hírében is állt, a király csak fenntartásokkal bízott benne:
– Találj egy jó párosítást – követelte ellentmondást nem tűrve, – különben életed végéig egy barlangban fogsz raboskodni!
Merlinnek ez alkalommal szerencséje volt: természetfeletti képességeit latba vetve áttekintette a huszadik század elején megjelent szakirodalmat, és talált egy jó érvet, amely – egyszerű földi halandók számára is – alátámasztotta, hogy a nagyszabású terv nem valósítható meg. Visszatért hát a királyhoz, ahol éppen minden vendég jelen volt. Merlin kiválasztott 56 hölgyet, hogy álljon a terem egyik oldalára, a másik oldalra pedig 95 lovagot szólított ki, és megkérdezte:
– Szép hölgyek, van-e köztetek, aki ezen lovagok valamelyikéhez szívesen férjhez menne?
– Nincs! – felelték egyhangúan a hölgyek.
Merlin erre Arthurhoz fordult:
– Felséges király, hogy kívánhatod tőlem, hogy ennek az 56 hölgynek férjet találjak, amikor már csak 55 lovag jöhet szóba potenciális párként?
Így aztán a király, aki kiváló képzésben részesült, minek következtében a skatulyaelvet is jól ismerte, azonnal belátta, hogy lehetetlent kíván, és kegyesen útjára bocsátotta a varázslót.
Nem telt bele sok idő azonban, és a királyi koponyában újabb ötlet fogant. Észrevette ugyanis, hogy a híres kerek asztalnál felszolgált vacsorákat a 150 lovag soha nem tudta békésen végigülni, a szomszédok állandóan – gyakran a szó szoros értelmében is – hajba kaptak valamin. Arthur nem tudott efelett napirendre térni, újra magához rendelte tehát Merlint, és megparancsolta: találjon ki olyan ültetési rendet, amelyben mindenki két jó barátja között foglal helyet. A természetfeletti képességekkel rendelkező varázsló egy szempillantás alatt átlátta, hogy a 150! lehetséges ültetési rend egyike sem megfelelő, és ezt azonmód jelentette is a királynak. Mikor Arthur magyarázatot követelt, Merlin széttárta a karját:
– Uram, királyom, én lennék a legboldogabb, ha létezne egyszerű magyarázat, de csak azt tudom megerősíteni: lehetetlent kívánsz. Ti halandók ezt nem érthetitek meg, legfeljebb úgy, ha hátralévő életetek egészét az érveim hallgatásának szentelitek.
A királynak más tervei voltak hátralévő éveit illetően, így aztán beváltotta fenyegetését: Merlin azóta is befalazva sínylődik egy sötét barlangban – az alkalmazott matematikusok legnagyobb bánatára!
A mese tanulsága, hogy vannak a gráfoknak olyan tulajdonságai, amelyeknek fennállása – megfelelő „prezentációval” könnyen ellenőrizhető. Azt, hogy egy gráfban van teljes párosítás vagy Hamilton-kör,2 legkönnyebben úgy „bizonyíthatjuk be”, hogy mutatunk egyet. Azt, hogy egy páros gráfban nincs teljes párosítás, úgy „bizonyíthatjuk”, hogy megadjuk az egyik „oldal” pontjainak olyan X részhalmazát, amelynek – együttesen – a másik oldalon |X|-nél3 kevesebb szomszédja van. Az Olvasónak és a szigorú Arthur királynak egyaránt az alábbi ábrát ajánljuk figyelmébe.
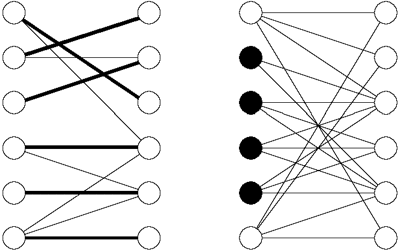
A jobb oldali gráfban van teljes párosítás (vastag vonalak jelölik), a bal oldaliban viszont nincs. Az utóbbi tényről a négy fekete pont (és szomszédsága) vizsgálatával győződhetünk meg.
A legtöbb gráfelméleti tulajdonság ilyen logikai struktúrával rendelkezik. Ha a tulajdonság fennállása könnyen bizonyítható (demonstrálható), akkor a számítógéptudósok a szóban forgó jellemzőt NP-tulajdonságnak nevezik.4 A Merlinnek feladott két probléma – a teljes párosításé és a Hamilton-köré – nyilvánvalóan NP-tulajdonságok. Ilyen tulajdonságokkal természetesen nemcsak a gráfelméletben, de a matematika szinte minden területén találkozunk. A természetes számok igen-igen fontos NP-tulajdonsága például az, hogy összetettek-e: ha egy n szám összetett, azt legkönnyebben egy n = ab felbontás megadásával támaszthatjuk alá (ahol természetesen a, b > 1).
Eddigi megjegyzéseink alapján nyilvánvaló, hogy miként kerülheti el Merlin a bezáratást azokban az esetekben, amelyekben a számára kitűzött feladatnak van megoldása. Tegyük fel például, hogy sikerült találnia a lovagok számára egy jó ültetési rendet. Ekkor nagyon könnyen meggyőzheti Arthurt, hogy valóban megoldotta a feladatot: le kell ültetni a lovagokat, és mindegyiktől meg kell kérdezni, elégedett-e e szomszédaival (vagy kivárni, hogy rendbontás nélkül ér-e véget a vacsora). Mindez pontosan annak felel meg, hogy a „baráti viszonyok gráfjának” az a tulajdonsága, hogy van benne Hamilton-kör, NP-tulajdonság. De akkor hogy lehet, hogy a házassági ügyben a varázsló megmenekült a bebörtönzéstől, az ültetés ügyében viszont kudarcot vallott, és őt magát ültették le (méghozzá örökre) – holott a két feladat közül egyiknek sem volt megoldása? Mi a különbség a teljes párosítás és a Hamilton-kör nemlétezése között? A mese alapján nyilván az Olvasó is kitalálta a választ: a teljes párosítás nemlétezése egy páros gráfnak NP-tulajdonsága, az viszont, hogy egy gráfban nincs Hamilton-kör, az a gráfnak nem NP-tulajdonsága. (Hogy pontosak legyünk: az utóbbi tényt egyelőre senki sem bizonyította be, de erős érvek szólnak amellett, hogy a helyzet a jövőben sem változik meg.)
Vannak tehát olyan NP-tulajdonságok, amelyeknek a fenn-nem-állása is NP-tulajdonság. Azokat a tételeket, amelyek egy NP-tulajdonság fennállásának és egy másik NP-tulajdonság fenn-nem-állásának ekvivalenciáját mondják ki, jó jellemzésnek nevezzük. Nevezetes jó jellemzésekkel a gráfelméletben és a matematika más területein is találkozhatunk.
Sok olyan NP-tulajdonság van, amely még ennél is kellemesebben viselkedik. A lovagok és a hölgyek összeházasításának problémájáról (mondjuk ennek a könyvnek az elolvasása után) akár maga Arthur is eldöntheti, hogy megoldható-e: nem kell mást tennie, mint követni a 10.4. alfejezetben leírt algoritmust. Ez persze sok időt és fáradságot kíván, de közönséges földi halandók is elvégezhetik, Merlin természetfeletti képességeire nincs hozzá szükség. Az efféle, effektív módon eldönthető tulajdonságokat P osztálybeli tulajdonságoknak nevezzük (a P a polinomiális időt rövidíti, ami az effektív módon való kiszámíthatóság pontos, de meglehetősen technikai jellemzése). Ebbe az osztályba tartozik gráfok több más – ebben a könyvben is vizsgált – tulajdonsága is, mint például az összefüggőség vagy egy kör létezése. Annak eldöntése, hogy egy szám prímszám-e vagy sem, szintén ilyen probléma – ezt nem sokkal e könyv nyomdába kerülése előtt sikerült bebizonyítani!
A polinomiális idő és az NP-tulajdonság fogalmának bevezetése jelenti a modern komplexitáselmélet kezdeteit. Az elmélet a tiszta és az alkalmazott matematika számos területét áthatja. A következő alfejezetekben bemutatjuk, miként alkalmazhatók a komplexitáselmélet gondolatai a kriptográfiában,5 az elméleti számítástudomány egyik legfontosabb területén.


